Alright math enthusiasts, gather ’round! Today, we’re diving deep into the heart of geometry with a classic: The Pythagorean Theorem Worksheet. This isn’t just another set of equations to memorize; it’s a fundamental concept that unlocks the relationship between the sides of a right triangle. Mastering the Pythagorean Theorem is crucial not only for academic success in math class but also for practical applications in fields like architecture, engineering, and even navigation. Think about it: calculating the length of a ramp, ensuring a building’s structural integrity, or even figuring out the shortest distance across a park – all rely on this powerful theorem.
So, what exactly is the Pythagorean Theorem? It states that in a right triangle (a triangle with one angle measuring 90 degrees), the square of the length of the hypotenuse (the side opposite the right angle) is equal to the sum of the squares of the lengths of the other two sides (called legs). Mathematically, we express this as: a² + b² = c², where ‘a’ and ‘b’ are the lengths of the legs, and ‘c’ is the length of the hypotenuse.
Why is it so important to practice with a Pythagorean Theorem worksheet? Because understanding the theorem conceptually is only half the battle. Application is key! Worksheets provide the opportunity to apply the theorem to various problems, solidifying your understanding and building your problem-solving skills. They also allow you to practice different scenarios, such as finding the length of the hypotenuse when you know the lengths of the legs, or finding the length of a leg when you know the length of the hypotenuse and the other leg. This type of practice is invaluable for building confidence and speed in solving Pythagorean Theorem problems. Furthermore, worksheets often present problems in different formats, including diagrams and word problems, which helps you develop the ability to identify right triangles in various contexts and apply the theorem appropriately.
Many students struggle with correctly identifying the hypotenuse and the legs of a right triangle, especially when the triangle is rotated or presented within a more complex diagram. They might also struggle with algebraic manipulation necessary to solve for a missing side length. A well-designed worksheet addresses these common challenges by providing a variety of problem types and visual aids. It encourages students to carefully analyze each problem, identify the knowns and unknowns, and apply the Pythagorean Theorem correctly. Regular practice with a Pythagorean Theorem worksheet is a sure way to overcome these obstacles and build a strong foundation in geometry.
Sample Pythagorean Theorem Worksheet Questions and Answers
Below are some sample questions that you might find on a Pythagorean Theorem Worksheet, along with their solutions. This is just a small glimpse into the kinds of problems you might encounter, but it gives you an idea of the practical application of the theorem.
Example Problems
Let’s tackle a few problems to illustrate how the Pythagorean Theorem works in practice:
- Problem 1: A right triangle has legs of length 3 and 4. Find the length of the hypotenuse.
- Problem 2: A right triangle has a hypotenuse of length 13 and one leg of length 5. Find the length of the other leg.
- Problem 3: A ladder 10 feet long leans against a wall. The base of the ladder is 6 feet away from the wall. How high up the wall does the ladder reach?
Answers to the Example Problems
Here are the answers to the problems listed above. Remember to show your work when solving similar problems on a worksheet!
-
Answer to Problem 1:
Using the Pythagorean Theorem: a² + b² = c²
3² + 4² = c²
9 + 16 = c²
25 = c²
c = √25 = 5
The length of the hypotenuse is 5.
-
Answer to Problem 2:
Using the Pythagorean Theorem: a² + b² = c²
5² + b² = 13²
25 + b² = 169
b² = 169 – 25
b² = 144
b = √144 = 12
The length of the other leg is 12.
-
Answer to Problem 3:
Using the Pythagorean Theorem: a² + b² = c²
In this case, the ladder is the hypotenuse (c = 10), the distance from the wall is one leg (a = 6), and the height up the wall is the other leg (b).
6² + b² = 10²
36 + b² = 100
b² = 100 – 36
b² = 64
b = √64 = 8
The ladder reaches 8 feet up the wall.
If you are looking for Pythagorean Triples – Definition, Formula, Examples, Facts you’ve visit to the right place. We have 20 Pics about Pythagorean Triples – Definition, Formula, Examples, Facts like Pythagorean (Pythagoras) Theorem – Definition, Formula, & Examples, Pythagorean Theorem – Definition, Formula & Examples | ChiliMath and also Pythagorean (Pythagoras) Theorem – Definition, Formula, & Examples. Read more:
Pythagorean Triples – Definition, Formula, Examples, Facts

www.splashlearn.com
Pythagorean Theorem Explained

www.pinterest.com
Pythagorean Theorem Examples And Answers
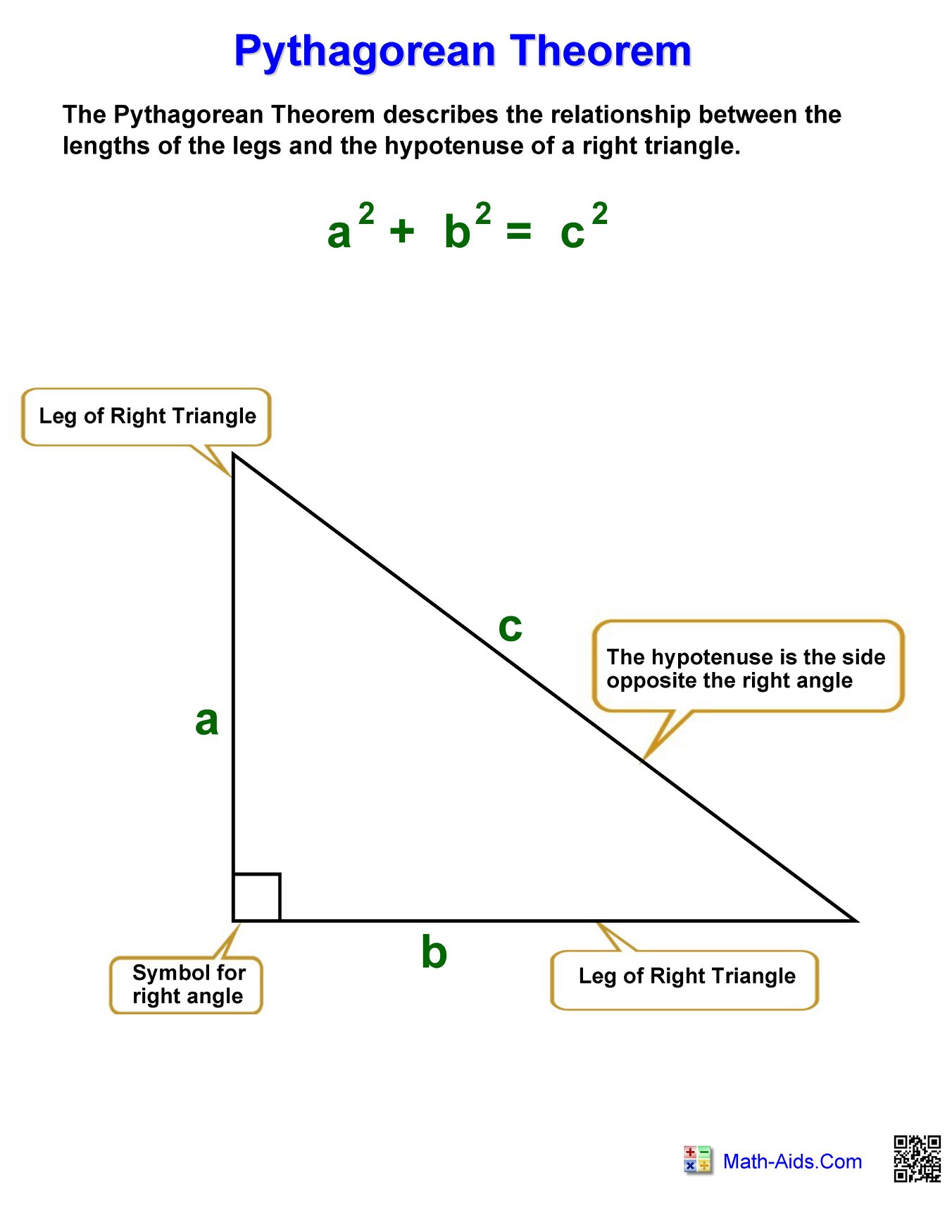
wentepuddblearning.z14.web.core.windows.net
Pythagorean Triples Formula- What Is Pythagorean Triples Formula? Examples

www.cuemath.com
The Pythagorean Theorem Of A Right Triangle Stock Illustration
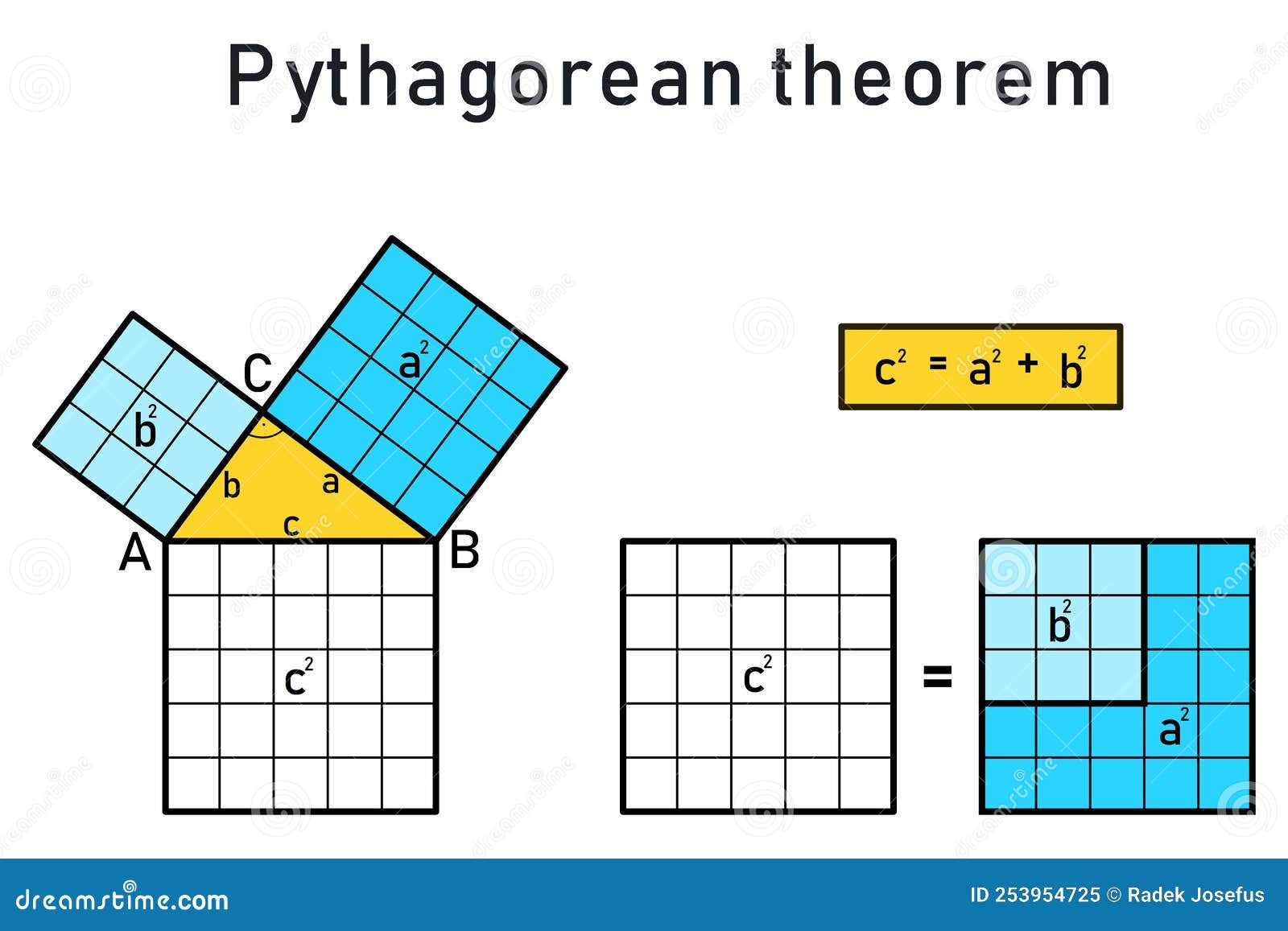
www.dreamstime.com
Pythagorean Theorem, Euclid Proof And Formula. Right Triangle. Basic
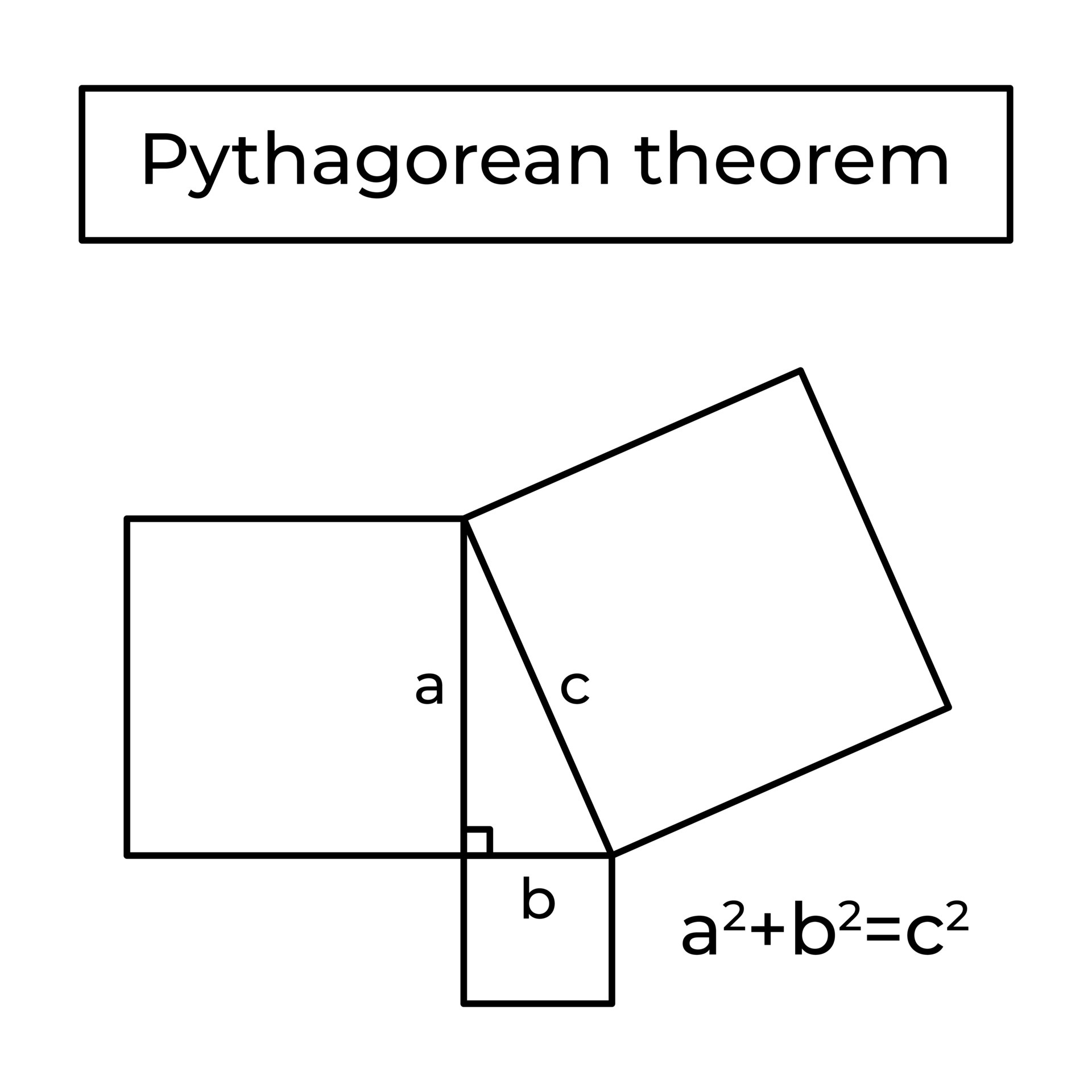
www.vecteezy.com
Geometry Pythagorean Theorem Examples At Steven Schrom Blog
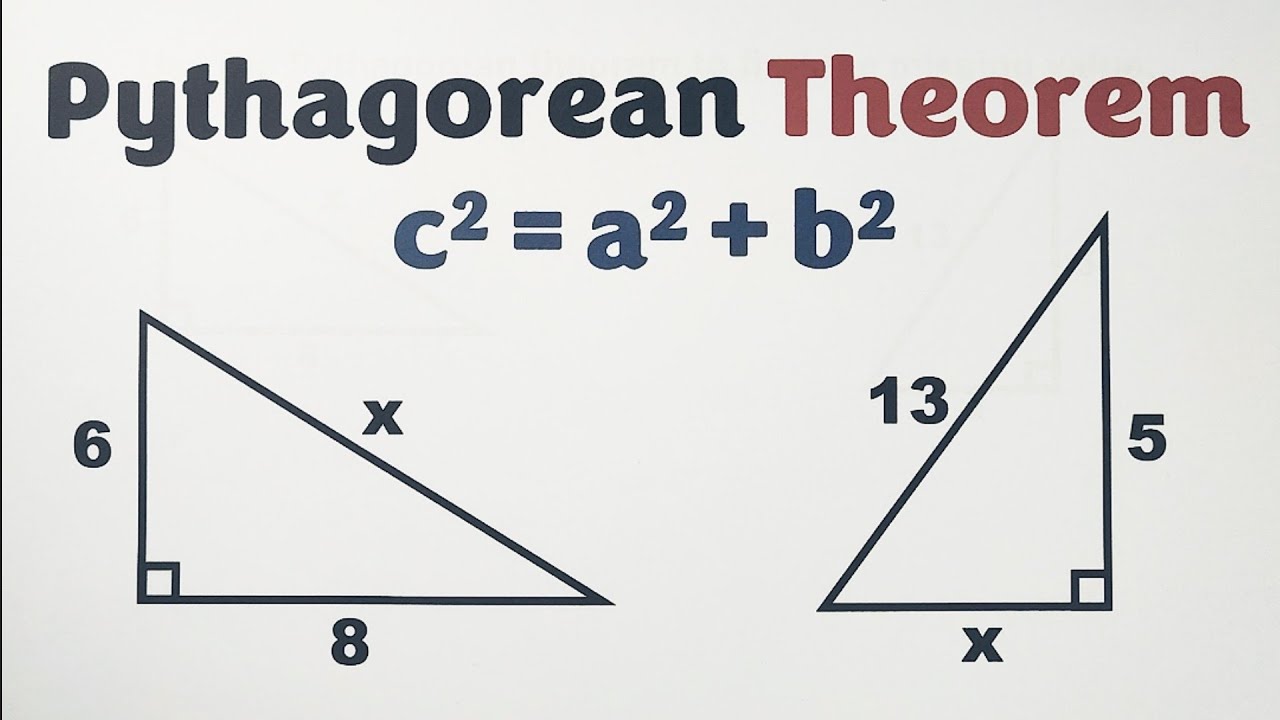
giohttgcr.blob.core.windows.net
What Is The Pythagorean Theorem

www.worksheetsplanet.com
How Do Civil Engineers Use The Pythagorean Theorem At Patrick Lakes Blog

storage.googleapis.com
Pythagorean Theorem – Definition, Formula & Examples | ChiliMath
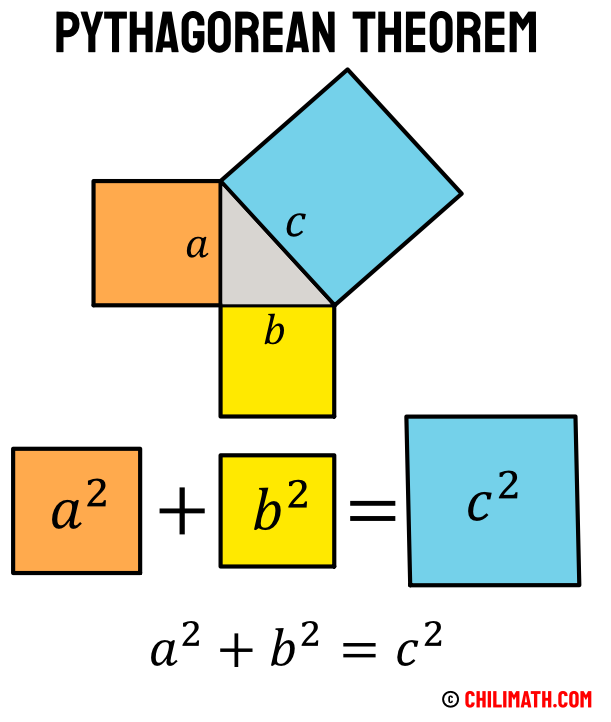
www.chilimath.com
Pythagorean Theorem – Vrogue.co
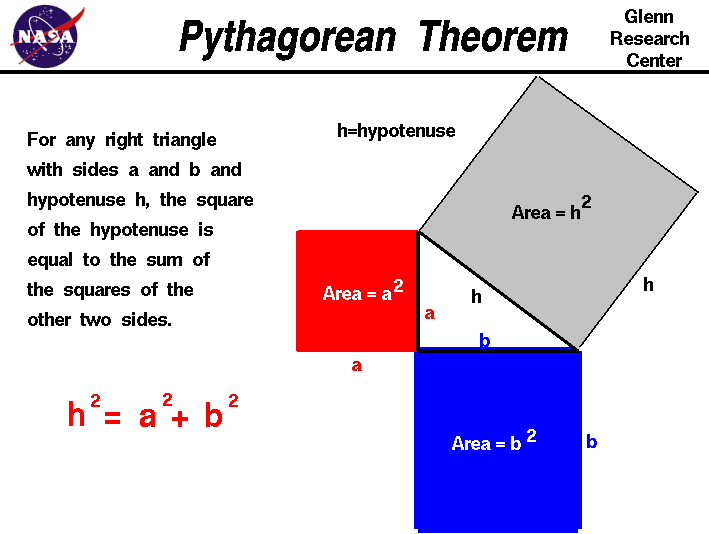
www.vrogue.co
Pythagorean Theorem Explained In 3d

printablelibataps.z19.web.core.windows.net
Pythagorean Equation Photos, Images & Pictures | Shutterstock

www.shutterstock.com
Pythagorean Theorem [Video] Formula, Definition, Examples & Proof
![Pythagorean Theorem [Video] Formula, Definition, Examples & Proof](https://static.tutors.com/assets/images/content/tutors-pythagorean-theorem-solve-for-c.jpg)
tutors.com
The Pythagorean Theorem States That The Hypotenuse Of A Right Triangle

www.dreamstime.com
Pythagorean Theorem Calculator – Steps To Solve – Inch Calculator

www.inchcalculator.com
The Pythagorean Theorem Was Created By Pythagoras, A Greek

www.pinterest.ph
Pythagorean Theorem – Definition, Formula & Examples | ChiliMath
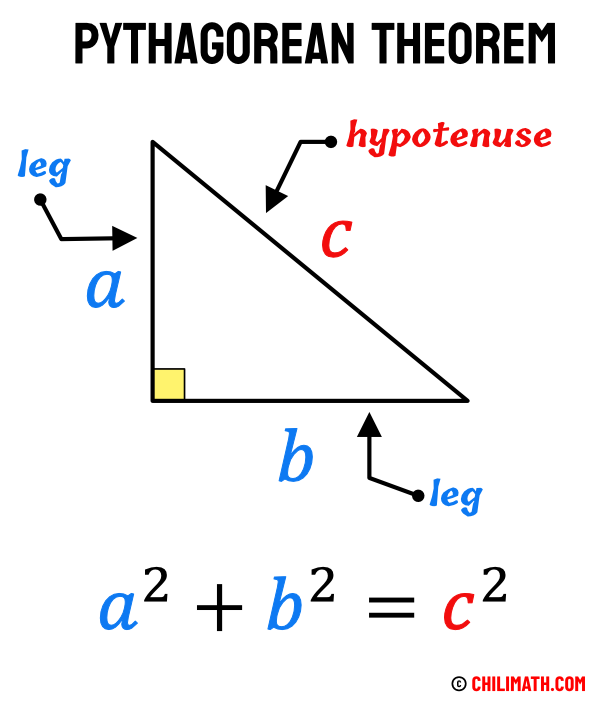
www.chilimath.com
Pythagorean (Pythagoras) Theorem – Definition, Formula, & Examples
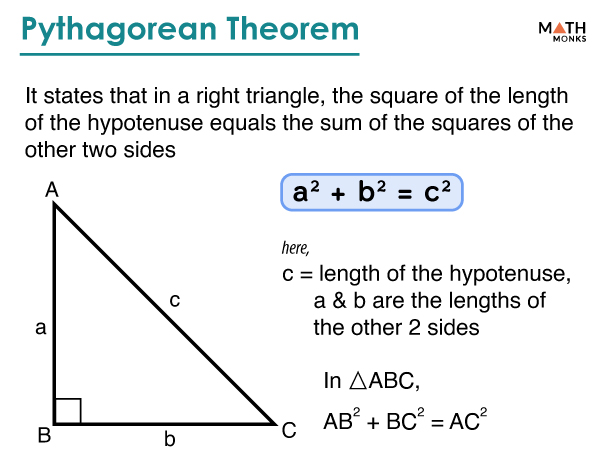
mathmonks.com
Geometry Pythagorean Theorem Examples At Steven Schrom Blog

giohttgcr.blob.core.windows.net
How do civil engineers use the pythagorean theorem at patrick lakes blog. Geometry pythagorean theorem examples at steven schrom blog. pythagorean theorem