Conquering geometry can feel like scaling a pyramid yourself! One of the trickiest yet most rewarding topics is calculating the volume of pyramids. That’s why a solid “Volume Of Pyramids Worksheet” is an invaluable tool for students of all levels. It helps solidify understanding through practical application, moving beyond rote memorization and fostering true conceptual grasp. Let’s dive into why these worksheets are so helpful and what you can expect to find in them.
Why Use a Volume Of Pyramids Worksheet?
A good worksheet offers several key benefits:
* **Reinforcement of Formula:** The core of calculating pyramid volume lies in understanding and applying the formula. Worksheets provide repeated practice to cement this formula in memory.
* **Application in Different Scenarios:** Pyramids come in various shapes and sizes. Worksheets present a range of problems involving different base shapes (squares, triangles, rectangles, etc.) and varying heights, forcing students to adapt their understanding.
* **Problem-Solving Skills:** Solving these problems hones critical thinking and problem-solving skills. Students learn to identify the necessary information, apply the correct formula, and arrive at the correct solution.
* **Error Identification:** Repeated practice allows students to identify common mistakes they might be making, such as confusing base area with side length, or forgetting to divide by three.
* **Visual Learning:** Many worksheets include diagrams and illustrations to help students visualize the pyramids and understand the relationship between the base, height, and volume.
What to Look For in a Quality Worksheet
Not all worksheets are created equal. Here’s what distinguishes a high-quality “Volume Of Pyramids Worksheet”:
* **Variety of Problems:** The worksheet should include problems with varying levels of difficulty, catering to different learning styles and comprehension levels. This includes problems with square, triangular, and rectangular bases, and potentially even more complex polygon bases.
* **Clear Instructions and Examples:** Clear and concise instructions are crucial. The worksheet should also include worked-out examples to guide students through the problem-solving process.
* **Diagrams and Visuals:** As mentioned before, visual aids are invaluable. Clear diagrams of the pyramids with labeled dimensions help students visualize the problem and avoid errors.
* **Answer Key:** A complete answer key is essential for self-assessment and immediate feedback. This allows students to check their work and identify areas where they need further practice.
* **Real-World Applications:** Some worksheets may include problems that relate to real-world scenarios, such as calculating the volume of a pyramid-shaped tent or a building, to make the concept more engaging.
By working through a well-designed “Volume Of Pyramids Worksheet,” students will gain confidence in their ability to calculate the volume of these fascinating geometric shapes. They will also develop essential problem-solving skills that will benefit them in future math courses and beyond. Remember, practice makes perfect, and a good worksheet is a key tool in achieving mastery!
Answers to Typical Volume Of Pyramids Worksheet Problems (Example Set)
To give you a taste of what to expect, here are the answers to some typical pyramid volume problems, presented in HTML list format for easy viewing. Note that these are *examples only* and the specific answers will depend on the problem sets within your chosen worksheet. We assume that volume is measured in cubic units, and lengths are measured in base unit:
- Problem 1: Square pyramid with base side length 6 units and height 8 units. Answer: 96 cubic units
- Problem 2: Triangular pyramid with base area 20 square units and height 9 units. Answer: 60 cubic units
- Problem 3: Rectangular pyramid with base length 8 units, width 5 units, and height 7 units. Answer: 93.33 cubic units (approximately)
- Problem 4: A pyramid with a base area of 45 square units and a volume of 135 cubic units. What is the height? Answer: 9 units
- Problem 5: A pyramid with a height of 12 units and a volume of 72 cubic units. What is the base area? Answer: 18 square units
If you are looking for Volume of a Cube (Formula + Example) you’ve came to the right place. We have 20 Pics about Volume of a Cube (Formula + Example) like What is Volume | Meaning & Definition, Volume – Definition, Formula, Examples and also Volume of a Rectangular Prism – Steps, Examples & Questions. Here it is:
Volume Of A Cube (Formula + Example)
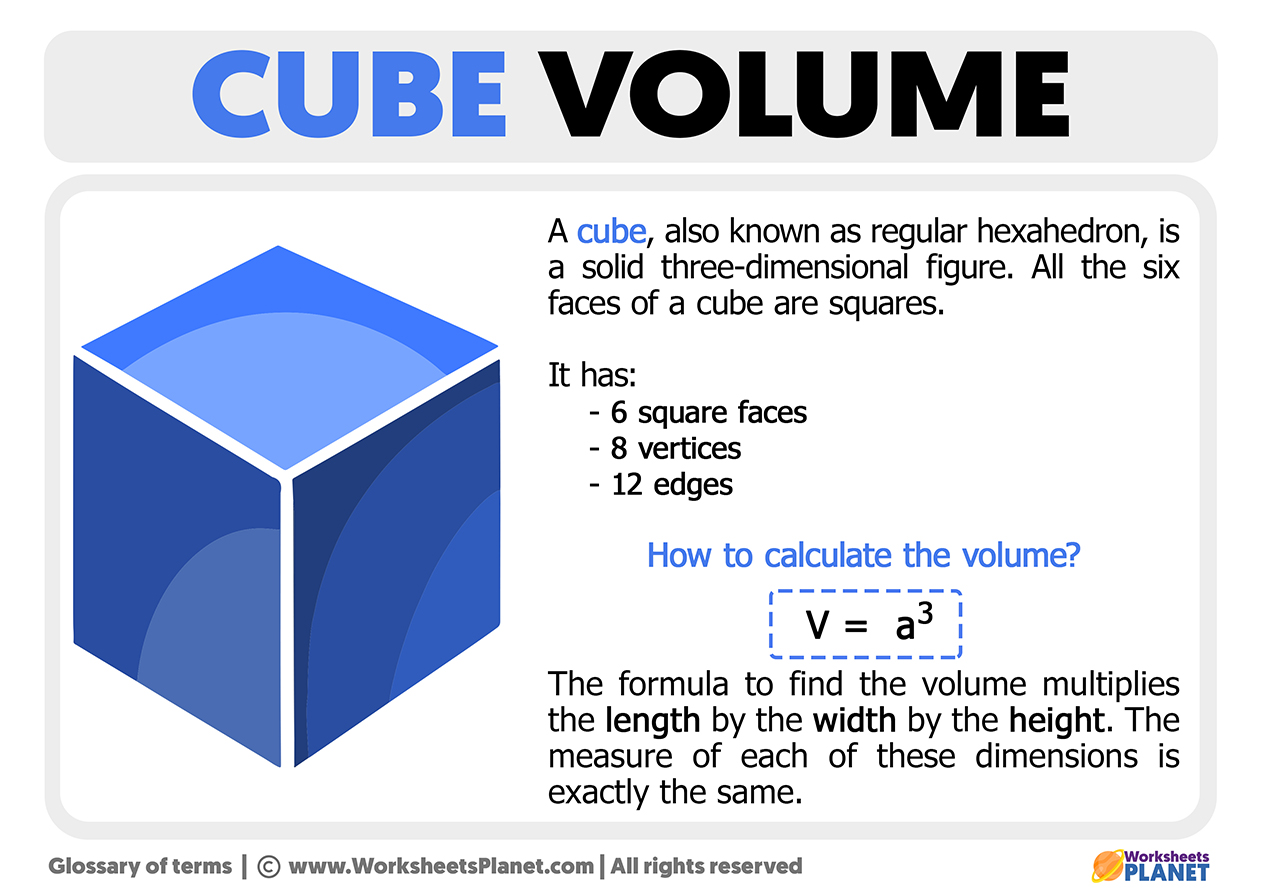
www.worksheetsplanet.com
Volume : Definition, Formula, Examples | GeeksforGeeks

www.geeksforgeeks.org
Volume Formula For A Rectangle
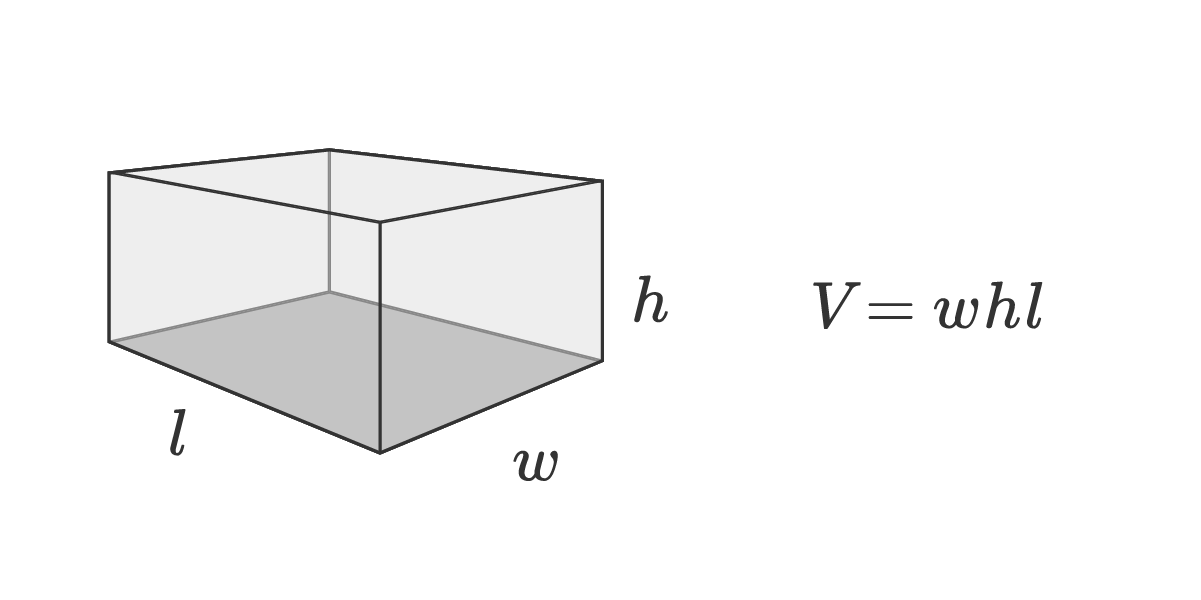
www.animalia-life.club
Volume Of A Cube – Formulas, Examples, And Diagrams
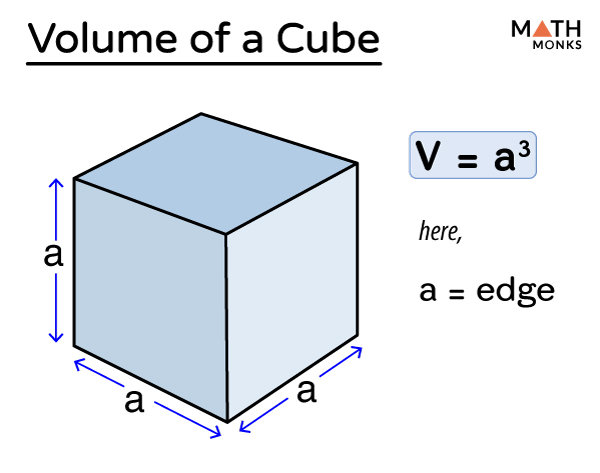
mathmonks.com
Volume Formula – GCSE Maths – Steps, Examples & Worksheet
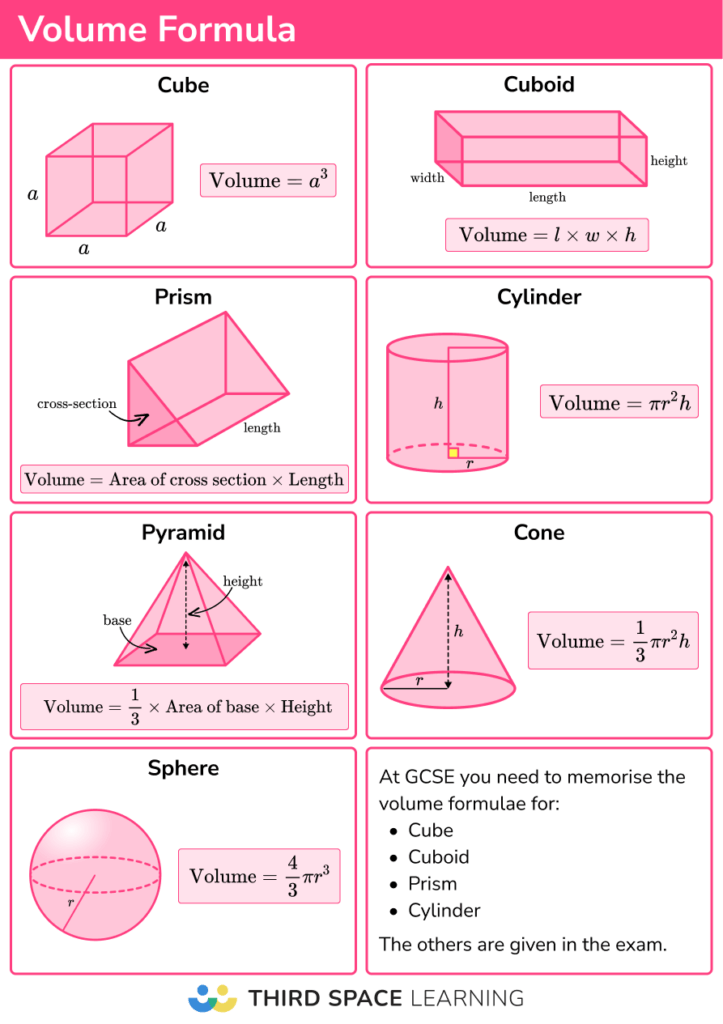
thirdspacelearning.com
Volume Of A Rectangular Prism – Steps, Examples & Questions
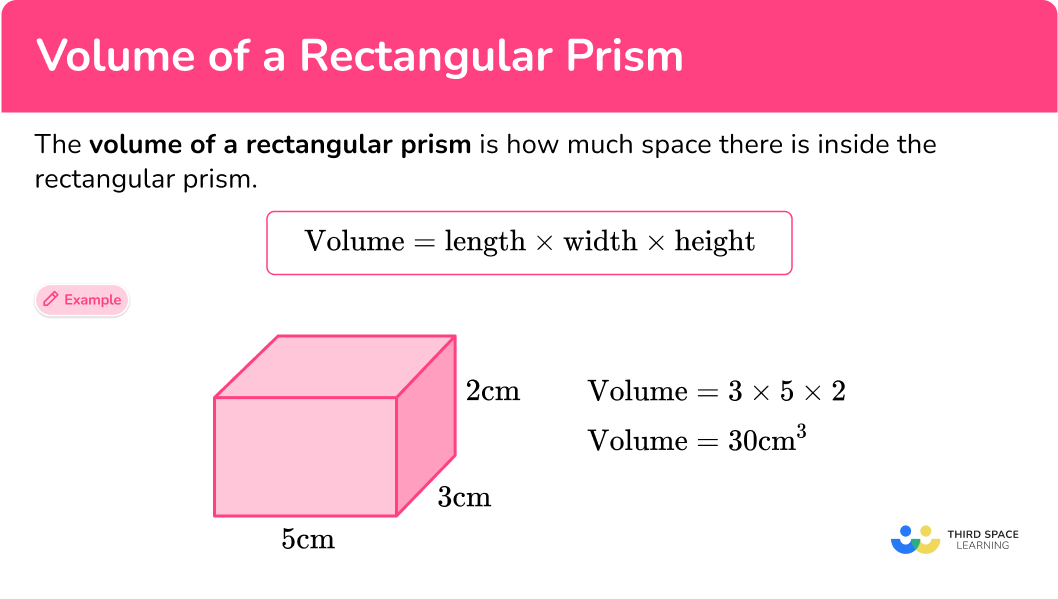
thirdspacelearning.com
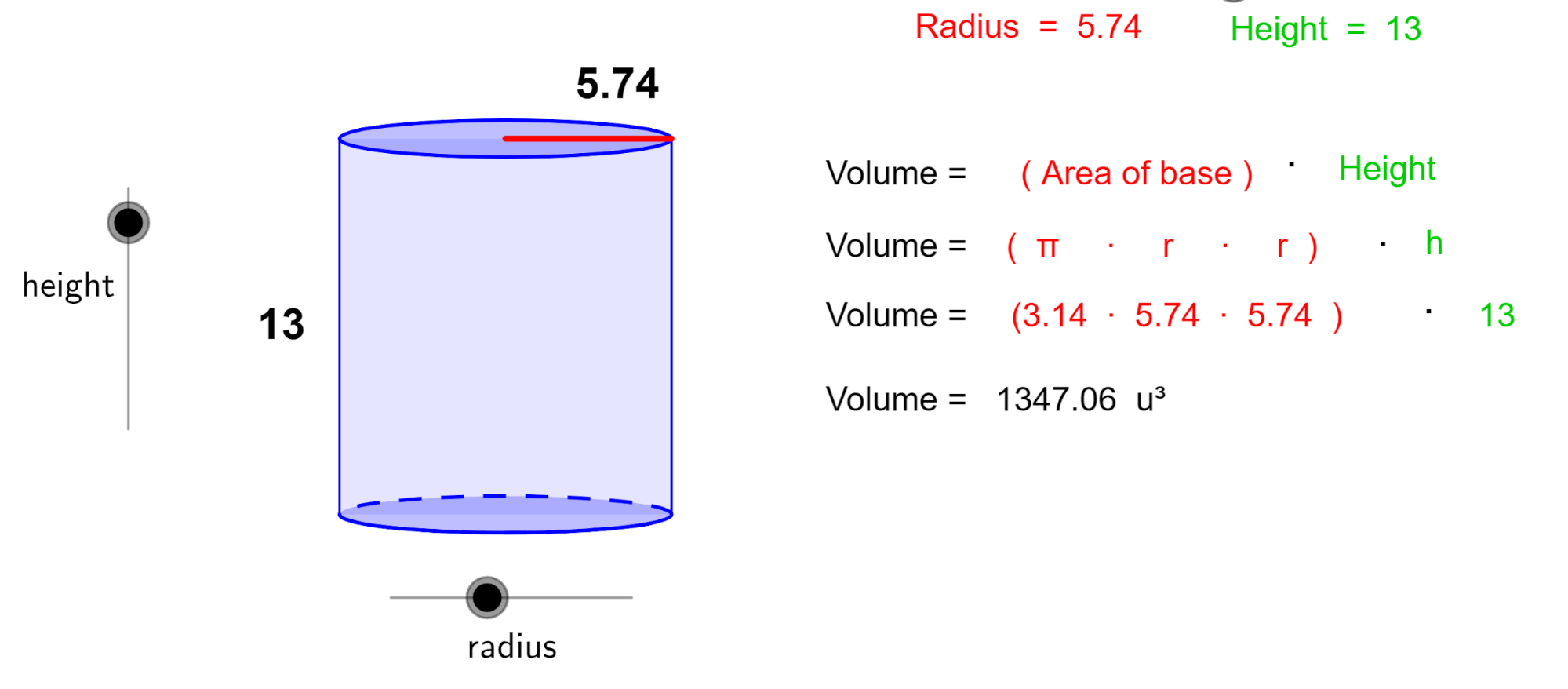
Volume Of A Cylinder (Formula + Example)

www.worksheetsplanet.com
Volume – Elementary Math Steps, Examples & Questions
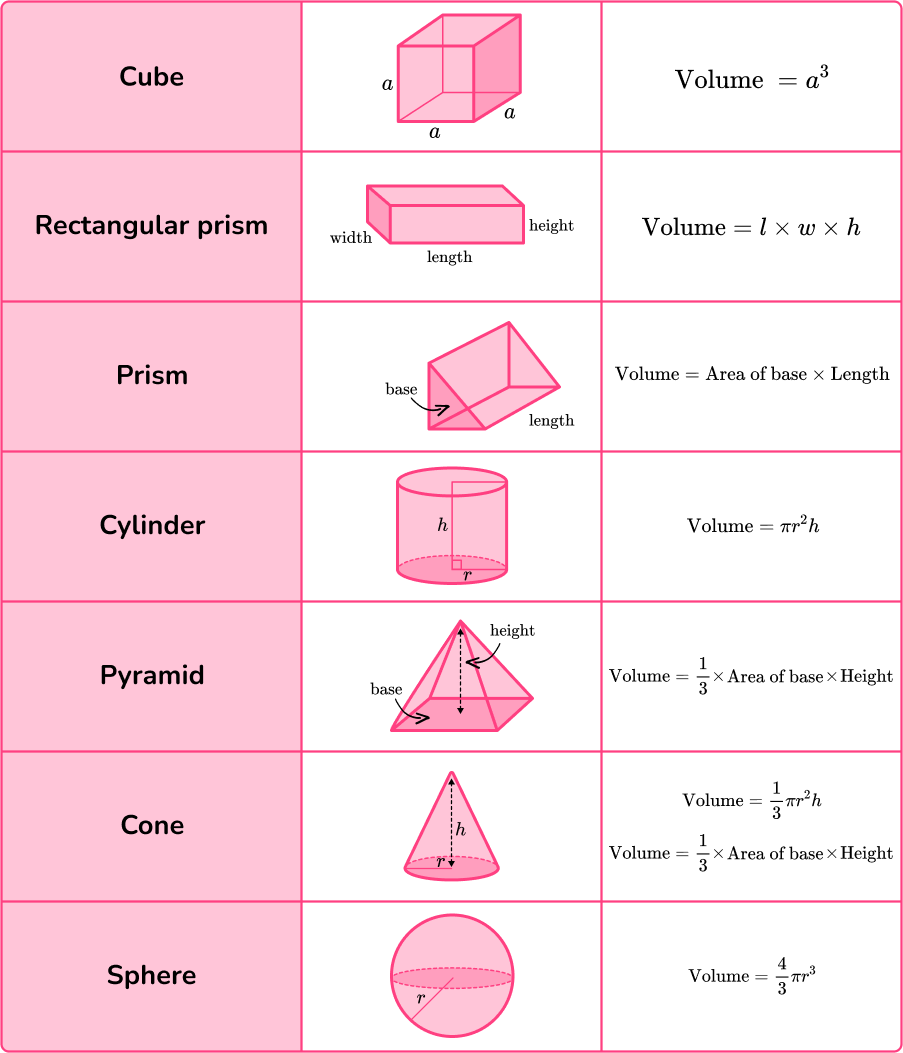
thirdspacelearning.com
Volume Of Sphere – Definition, Formula & Examples | ChiliMath
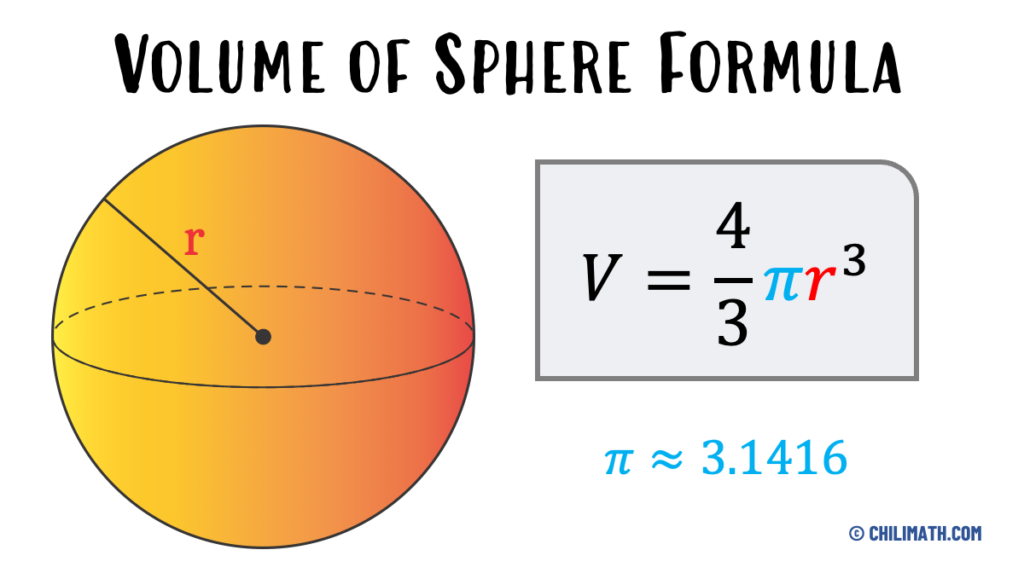
www.chilimath.com
Volume Of A Cube Calculator
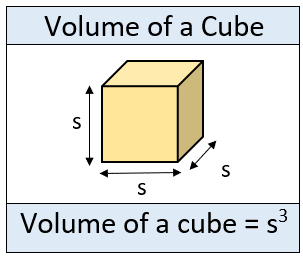
www.math-salamanders.com
Volume Formula – Explanation, Examples & Practice Questions

thirdspacelearning.com
Volume Formulas Sheet
classzonepatellate.z21.web.core.windows.net
What Is Volume? – Definition, Examples And Practice Questions
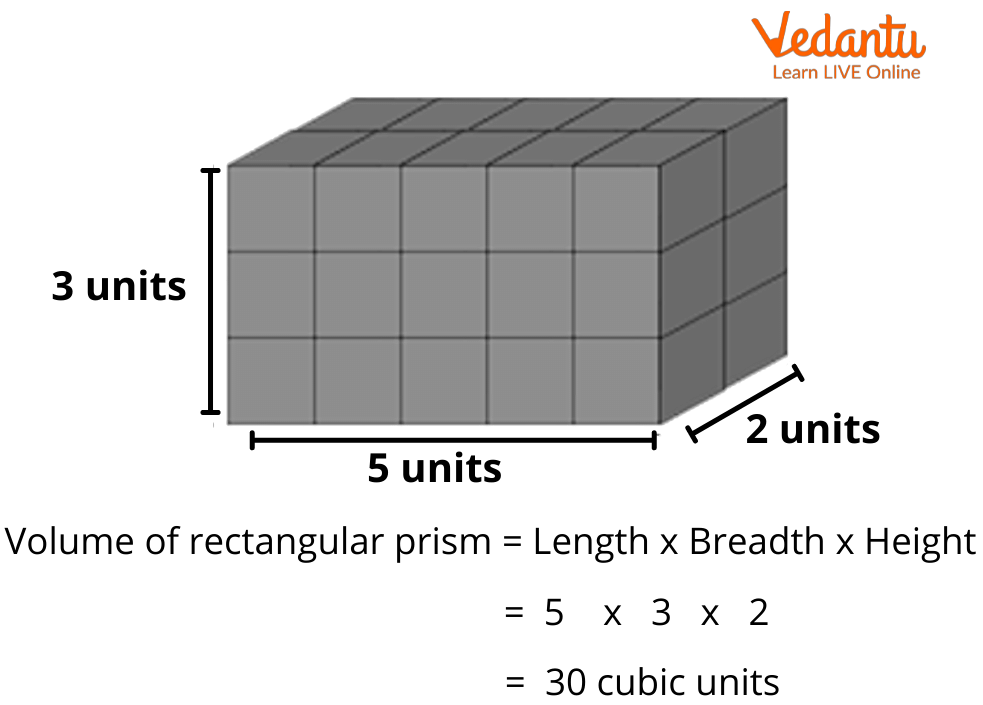
www.vedantu.com
Volume

ar.inspiredpencil.com
Volume Formula – GCSE Maths – Steps, Examples & Worksheet

thirdspacelearning.com
What Is Volume | Meaning & Definition

www.worksheetsplanet.com
Volume Of A Cube – Math Steps, Formula, Examples & Questions
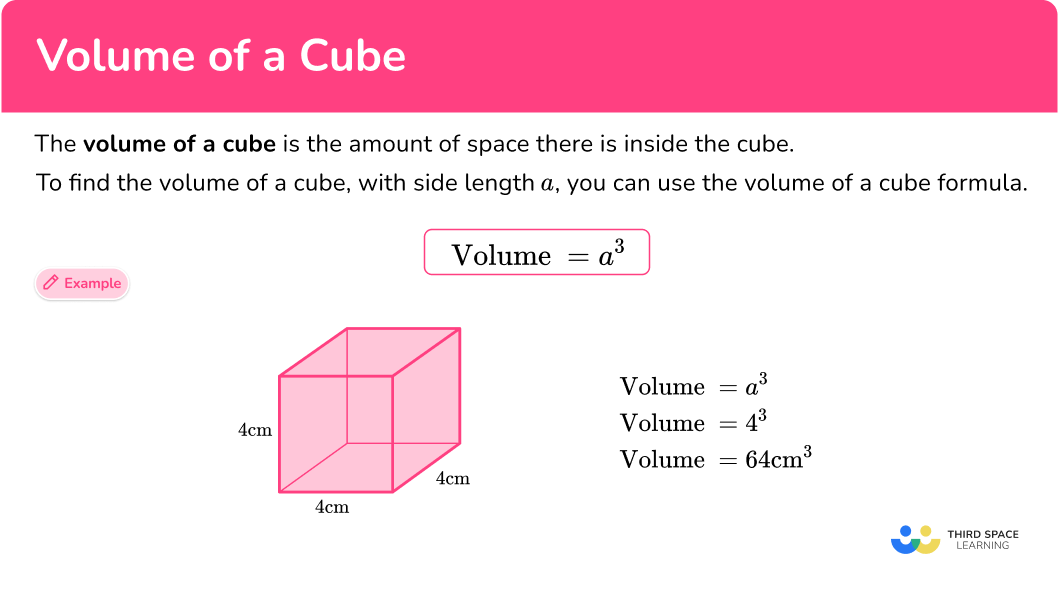
thirdspacelearning.com
How Do You Find Volume In A Pyramid – Printable Templates Free
read.cholonautas.edu.pe
Volume – Definition, Formula, Examples

brighterly.com
How To Calculate Volume From Area And Thickness At Timothy Mears Blog

storage.googleapis.com
volume formulas sheet. volume of a cube (formula + example). Volume of sphere